Skip to contents

estimatr in the Tidyverse

Shikhar Singh

Source: ../vignettes/estimatr-in-the-tidyverse.Rmd
estimatr-in-the-tidyverse.Rmd

estimatr is for (fast) OLS and IV regression with robust standard errors. This document shows how estimatr integrates with RStudio’s tidyverse suite of packages.

We use the Swiss Fertility and Socioeconomic Indicators data (available in R, description here) to show how lm_robust works with dplyr, ggplot2, and purrr. What is shown for lm_robust here typically applies to all the other estimatr functions (lm_robust, difference_in_mean, lm_lin, iv_robust, and horovitz_thompson).

Getting tidy

The first step to the tidyverse is turning model output into data we can manipulate. The tidy function converts an lm_robust object into a data.frame.

library(estimatr)
fit <- lm_robust(Fertility ~ Agriculture + Catholic, data = swiss)
tidy(fit)
##          term   estimate  std.error statistic      p.value    conf.low
## 1 (Intercept) 59.8639237 5.47384281 10.936361 3.934173e-14 48.83211840
## 2 Agriculture  0.1095281 0.10305115  1.062852 2.936478e-01 -0.09815783
## 3    Catholic  0.1149621 0.03854836  2.982283 4.651169e-03  0.03727301
##    conf.high df   outcome
## 1 70.8957290 44 Fertility
## 2  0.3172141 44 Fertility
## 3  0.1926512 44 Fertility

Data manipulation with dplyr

Once a regression fit is a data.frame, you can use any of the dplyr “verbs” for data manipulation, like mutate,filter, select, summarise, group_by, and arrange (more on this here).

library(tidyverse)

# lm_robust and filter
fit %>% tidy %>% filter(term == "Agriculture")
##          term  estimate std.error statistic   p.value    conf.low conf.high df
## 1 Agriculture 0.1095281 0.1030511  1.062852 0.2936478 -0.09815783 0.3172141 44
##     outcome
## 1 Fertility
# lm_robust and select
fit %>% tidy %>% select(term, estimate, std.error)
##          term   estimate  std.error
## 1 (Intercept) 59.8639237 5.47384281
## 2 Agriculture  0.1095281 0.10305115
## 3    Catholic  0.1149621 0.03854836
# lm_robust and mutate
fit %>% tidy %>% mutate(t_stat = estimate/ std.error,
                        significant = p.value <= 0.05)
##          term   estimate  std.error statistic      p.value    conf.low
## 1 (Intercept) 59.8639237 5.47384281 10.936361 3.934173e-14 48.83211840
## 2 Agriculture  0.1095281 0.10305115  1.062852 2.936478e-01 -0.09815783
## 3    Catholic  0.1149621 0.03854836  2.982283 4.651169e-03  0.03727301
##    conf.high df   outcome    t_stat significant
## 1 70.8957290 44 Fertility 10.936361        TRUE
## 2  0.3172141 44 Fertility  1.062852       FALSE
## 3  0.1926512 44 Fertility  2.982283        TRUE

Data visualization with ggplot2

ggplot2 offers a number of data visualization tools that are compatible with estimatr

  1. Make a coefficient plot:
fit %>% 
  tidy %>% 
  filter(term != "(Intercept)") %>%
  ggplot(aes(y = term, x = estimate)) + 
  geom_vline(xintercept = 0, linetype = 2) + 
  geom_point() + 
  geom_errorbarh(aes(xmin = conf.low, xmax = conf.high, height = 0.1)) + 
  theme_bw()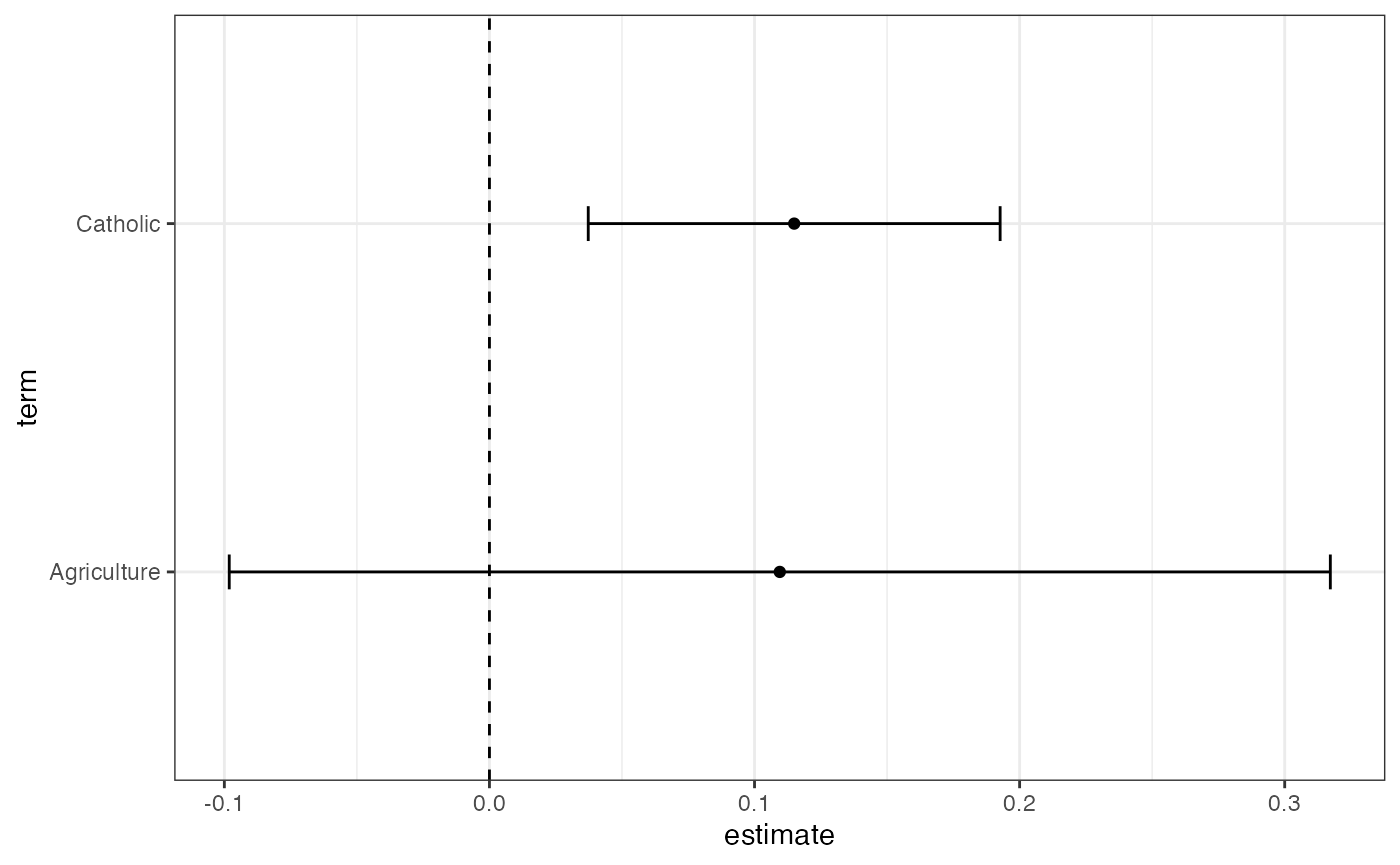

  1. Put CIs based on robust variance estimates (rather than the “classical” variance estimates) with the geom_smooth and stat_smooth functions.
library(ggplot2)
ggplot(swiss, aes(x = Agriculture, y = Fertility)) +
  geom_point() +
  geom_smooth(method = "lm_robust") +
  theme_bw()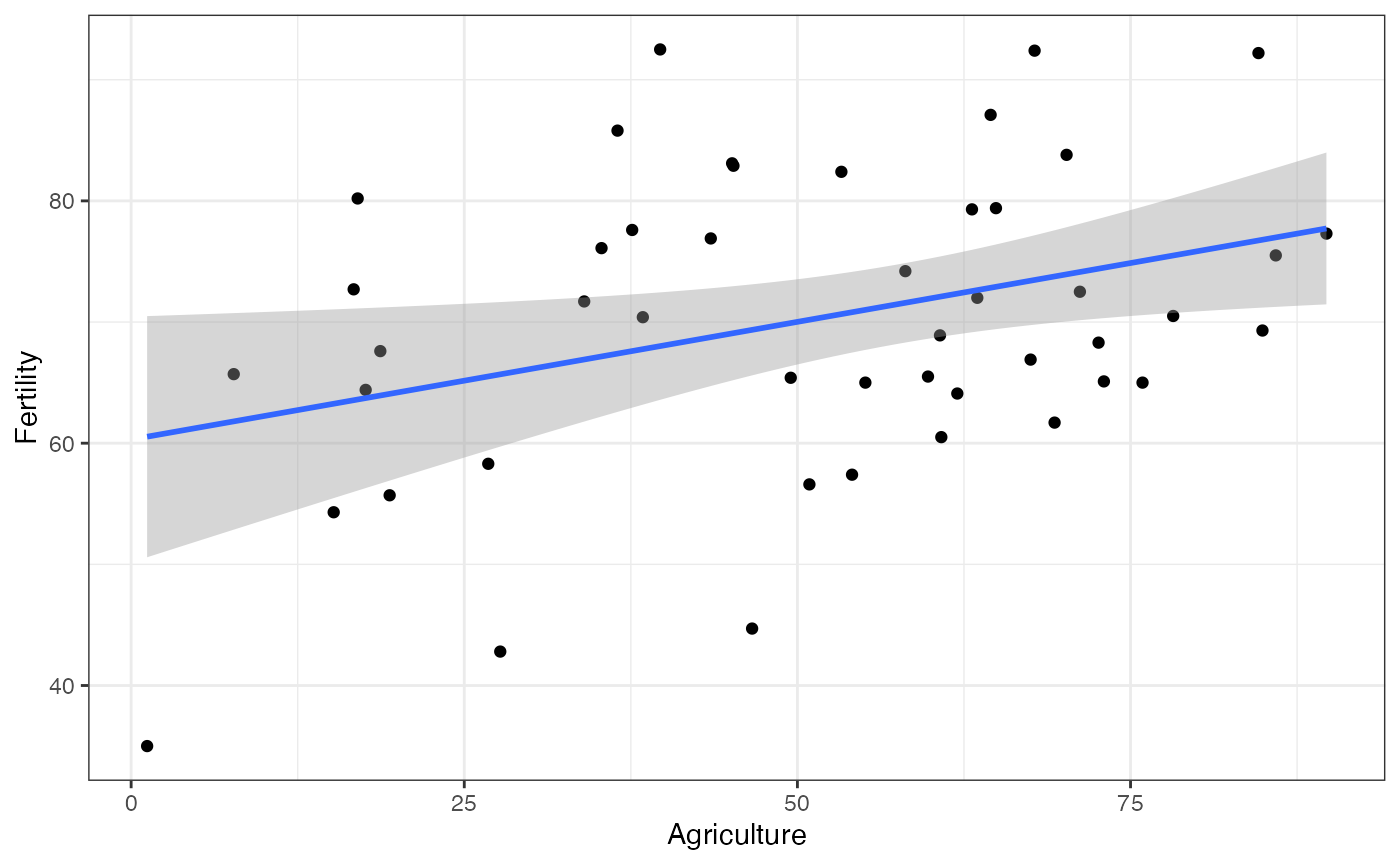

Note that the functional form can include polynomials. For instance, if the model is \(Fertility \sim Agriculture + Agriculture^2 + Agriculture^3\), we can model this in the following way:

library(ggplot2)
ggplot(swiss, aes(x = Agriculture, y = Fertility)) +
  geom_point() +
  geom_smooth(method = "lm_robust",
              formula = y ~ poly(x, 3, raw = TRUE)) +
  theme_bw()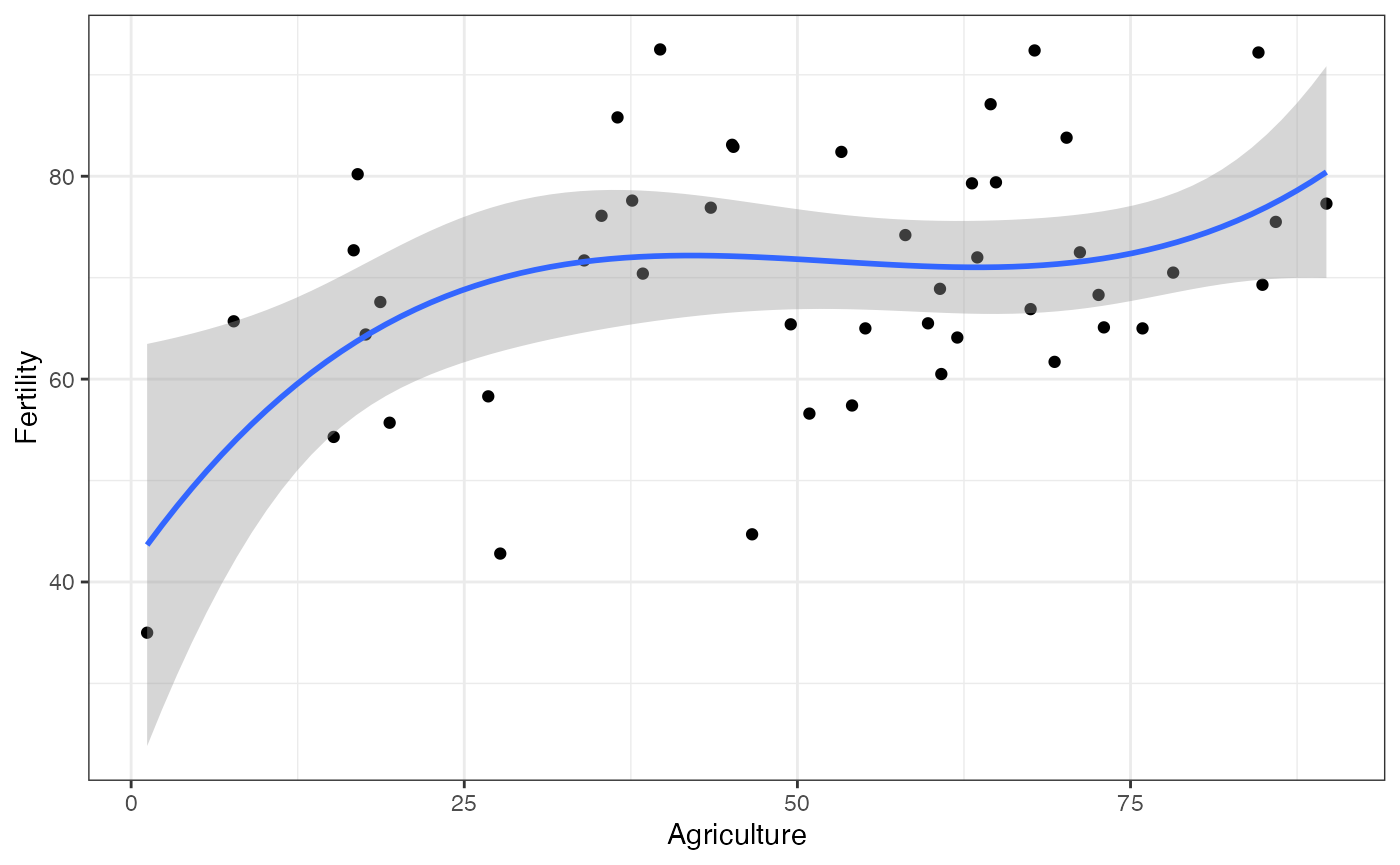

Bootstrap using rsample

The rsample pacakage provides tools for bootstrapping:

library(rsample)

boot_out <-
  bootstraps(data = swiss, 500)$splits %>%
  map(~ lm_robust(Fertility ~ Catholic + Agriculture, data = analysis(.))) %>% 
  map(tidy) %>%
  bind_rows(.id = "bootstrap_replicate")
kable(head(boot_out))
bootstrap_replicate term estimate std.error statistic p.value conf.low conf.high df outcome
1 (Intercept) 66.6445111 6.1805580 10.7829278 0.0000000 54.1884149 79.1006074 44 Fertility
1 Catholic 0.0559302 0.0346962 1.6119974 0.1141134 -0.0139954 0.1258558 44 Fertility
1 Agriculture 0.0613375 0.1123003 0.5461920 0.5876929 -0.1649889 0.2876639 44 Fertility
2 (Intercept) 67.4618025 2.7822907 24.2468562 0.0000000 61.8544640 73.0691410 44 Fertility
2 Catholic 0.1720616 0.0238761 7.2064269 0.0000000 0.1239424 0.2201808 44 Fertility
2 Agriculture -0.0433626 0.0515919 -0.8404923 0.4051767 -0.1473392 0.0606140 44 Fertility

boot_out is a data.frame that contains estimates from each boostrapped sample. We can then use dplyr functions to summarize the bootstraps, tidyr functions to reshape the estimates, and GGally::ggpairs to visualize them.

boot_out %>%
  group_by(term) %>%
  summarise(boot_se = sd(estimate))
## # A tibble: 3 × 2
##   term        boot_se
##   <chr>         <dbl>
## 1 (Intercept)  5.45  
## 2 Agriculture  0.102 
## 3 Catholic     0.0365
# To visualize the sampling distribution

library(GGally)
boot_out %>% 
  select(bootstrap_replicate, term, estimate) %>%
  spread(key = term, value = estimate) %>%
  select(-bootstrap_replicate) %>%
  ggpairs(lower = list(continuous = wrap("points", alpha = 0.1))) +
  theme_bw()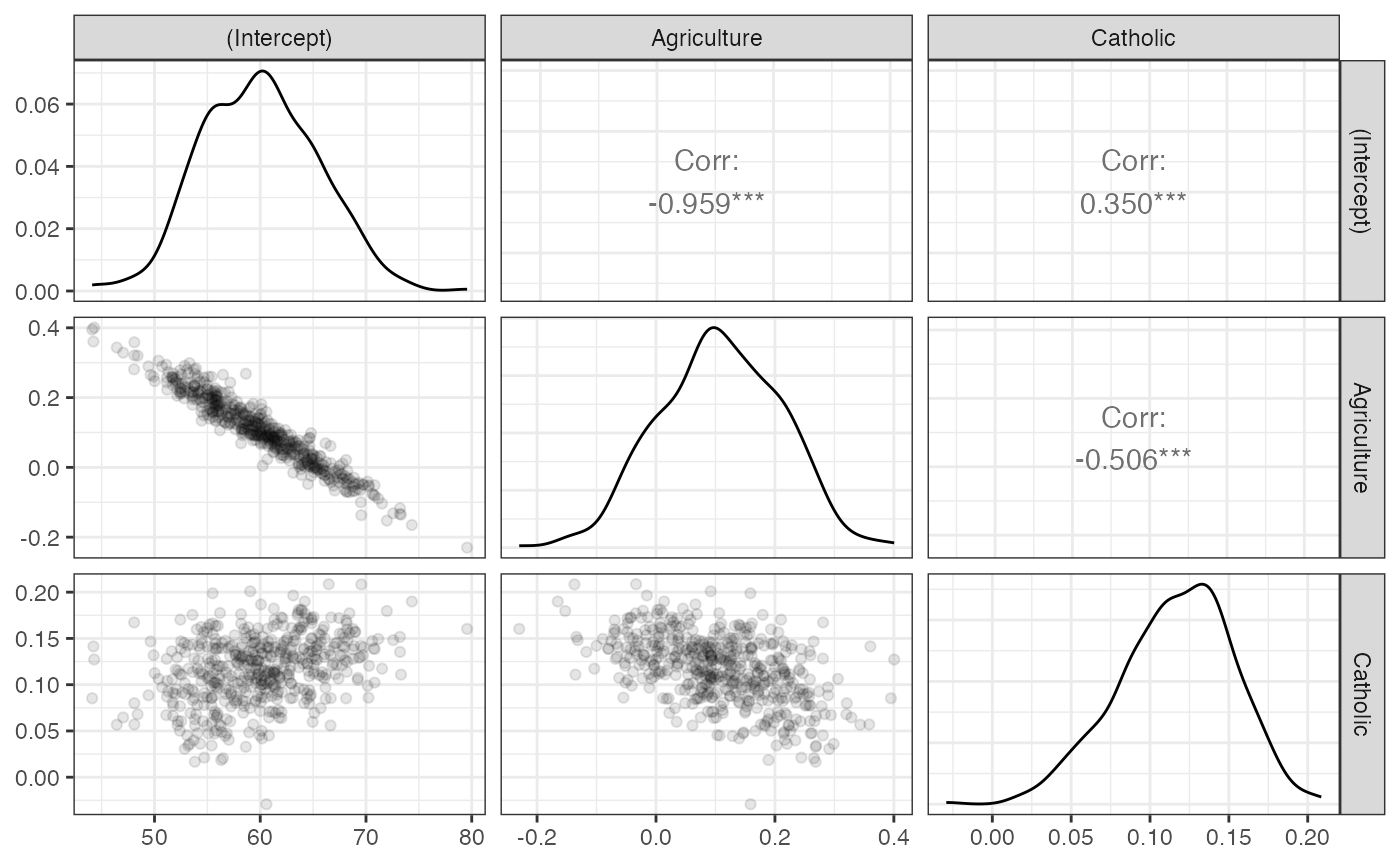

Multiple models using purrr

purrr provides tools to perform the same operation on every element of a vector. For instance, we may want to estimate a model on different subsets of data. We can use the map function to do this.

library(purrr)

# Running the same model for highly educated and less educated cantons/districts

two_subsets <- 
  swiss %>%
  mutate(HighlyEducated = as.numeric(Education > 8)) %>%
  split(.$HighlyEducated) %>%
  map( ~ lm_robust(Fertility ~ Catholic, data = .)) %>%
  map(tidy) %>%
  bind_rows(.id = "HighlyEducated")

kable(two_subsets, digits =2)
HighlyEducated term estimate std.error statistic p.value conf.low conf.high df outcome
0 (Intercept) 68.41 1.89 36.27 0.00 64.50 72.31 23 Fertility
0 Catholic 0.14 0.03 4.20 0.00 0.07 0.20 23 Fertility
1 (Intercept) 62.41 2.63 23.74 0.00 56.93 67.89 20 Fertility
1 Catholic 0.06 0.08 0.71 0.48 -0.11 0.23 20 Fertility

Alternatively, we might want to regress different dependent variables on the same independent variable. map can be used alongwith estimatr functions for this purpose as well.

three_outcomes <-
  c("Fertility", "Education", "Agriculture") %>%
  map(~ formula(paste0(., " ~ Catholic"))) %>%
  map(~ lm_robust(., data = swiss)) %>%
  map_df(tidy)

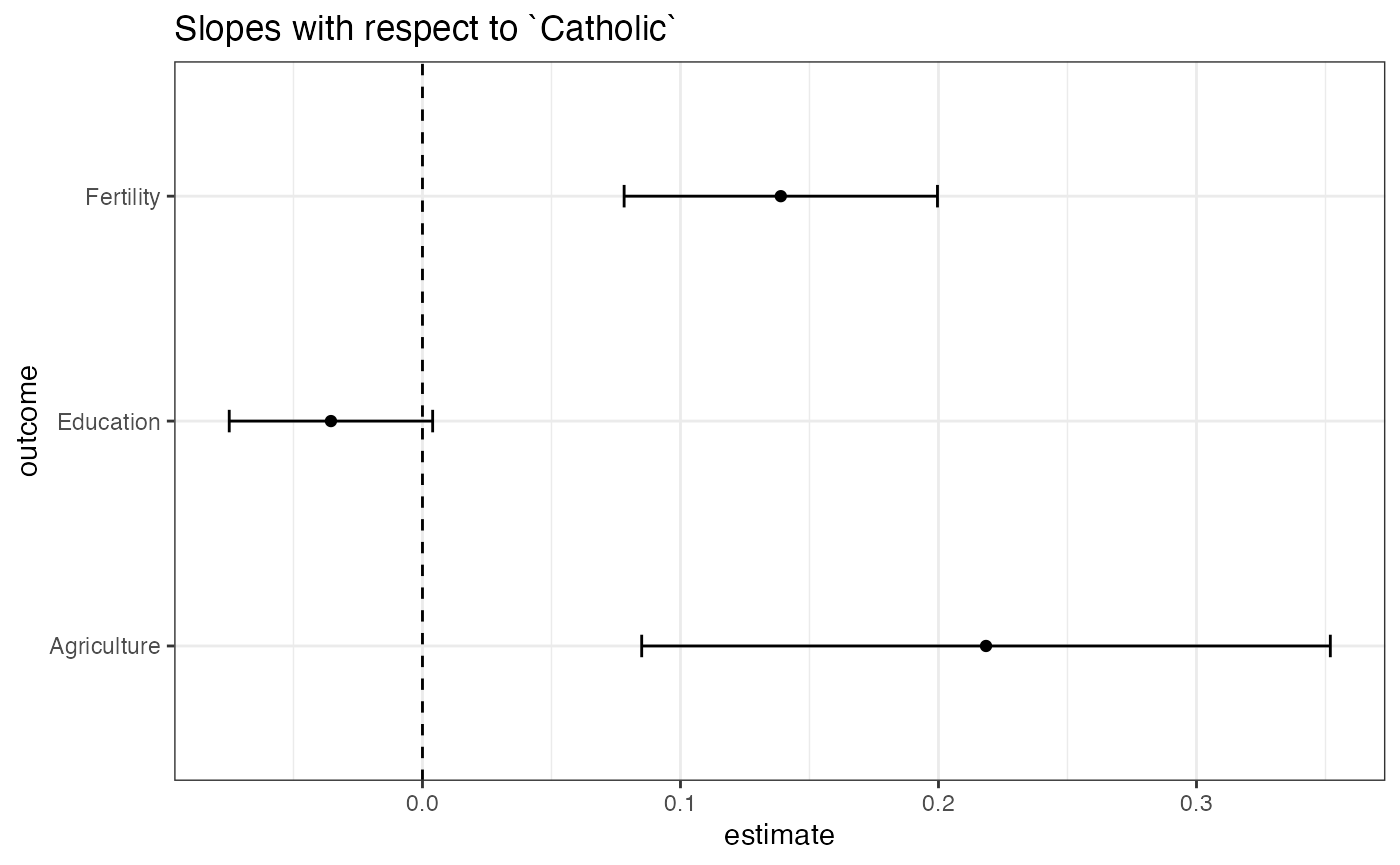
kable(three_outcomes, digits =2)
term estimate std.error statistic p.value conf.low conf.high df outcome
(Intercept) 64.43 1.78 36.11 0.00 60.83 68.02 45 Fertility
Catholic 0.14 0.03 4.61 0.00 0.08 0.20 45 Fertility
(Intercept) 12.44 1.73 7.20 0.00 8.96 15.92 45 Education
Catholic -0.04 0.02 -1.81 0.08 -0.07 0.00 45 Education
(Intercept) 41.67 4.46 9.35 0.00 32.69 50.65 45 Agriculture
Catholic 0.22 0.07 3.30 0.00 0.08 0.35 45 Agriculture

Using ggplot2, we can make a coefficient plot:

three_outcomes %>%
  filter(term == "Catholic") %>%
  ggplot(aes(x = estimate, y = outcome)) +
  geom_vline(xintercept = 0, linetype = 2) +
  geom_point() + 
  geom_errorbarh(aes(xmin = conf.low, xmax = conf.high, height = 0.1)) + 
  ggtitle("Slopes with respect to `Catholic`") + 
  theme_bw()

Concluding thoughts

Using estimatr functions in the tidyverse is easy once the model outputs have been turned into data.frames. We accomplish this with the tidy function. After that, so many summary and visualization possibilities open up. Happy tidying!