This document shows some things researchers may wish to add to their preanalysis plans using design declaration and diagnosis.

Setup

Declare the Design

program two_arm_design, rclass
  
  syntax [, sample_size(integer 100) effect_size(real .5) number_treated(integer 50)]
    
  drop _all
  
  * // Model
  
  * Population
  
  set obs `sample_size'
  
  gen noise = rnormal(0, 1)
  
  * Potential outcomes
  
  gen Y_Z_0 = noise
  gen Y_Z_1 = noise + `effect_size'
  
  * // Inquiry 

  return scalar estimand = `effect_size'
  
  * // Data strategy
  
  * Assignment strategy
  
  complete_ra Z, m(`number_treated')
  
  * Reveal outcomes
  
  gen     Y = Y_Z_0 
  replace Y = Y_Z_1 if Z == 1
  
  * // Answer strategy
  
  reg Y Z, vce(hc2)
  
  matrix b = e(b)
    
  return scalar estimate = b[1, 1]
  
  return scalar p_value = 2 * ttail(e(df_r), abs(_b[Z]/_se[Z]))

end

Mock Figure

. two_arm_design

. twoway (scatter Y Z)

Mock Regression Table

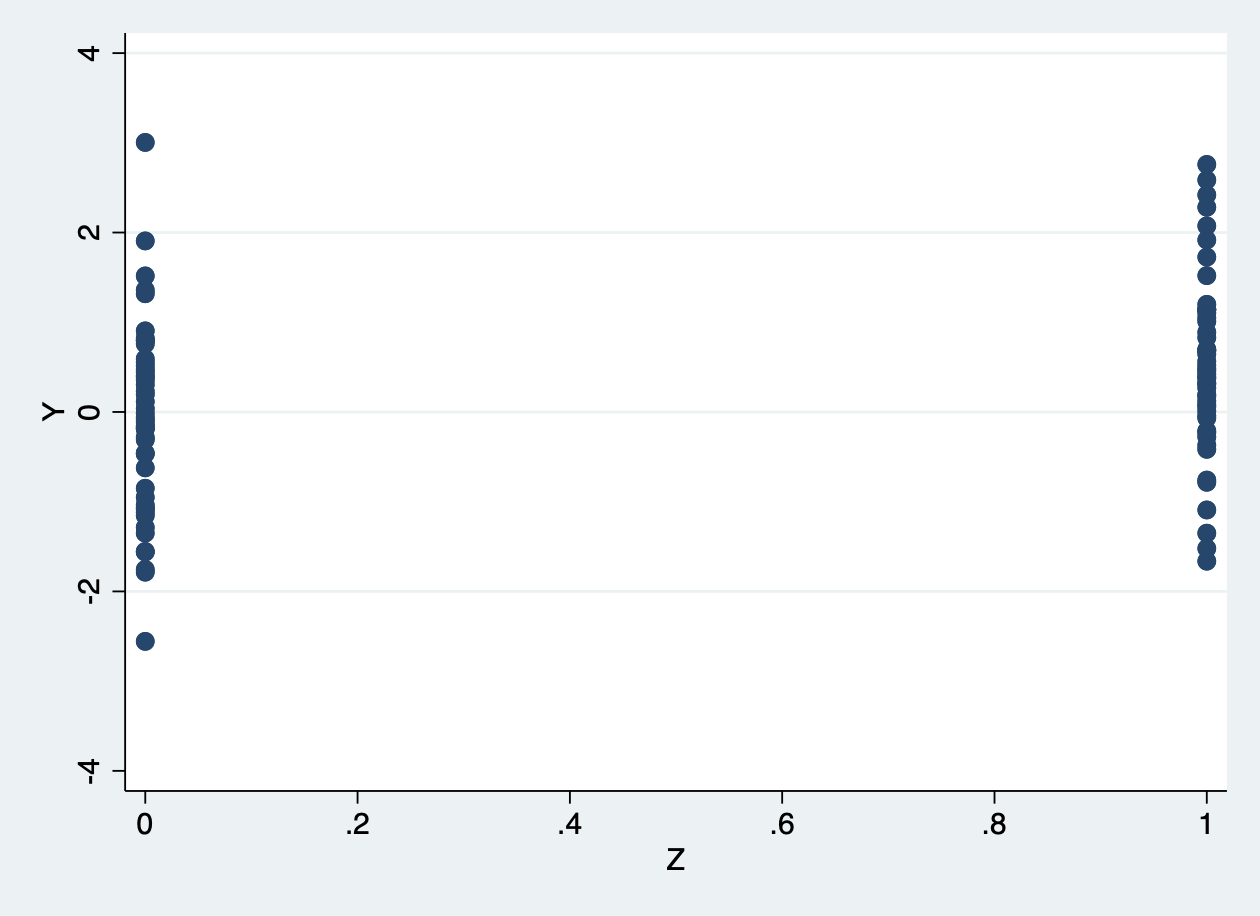
. reg Y Z, vce(hc2)

Linear regression                               Number of obs     =        100
                                                F(1, 98)          =       8.53
                                                Prob > F          =     0.0043
                                                R-squared         =     0.0801
                                                Root MSE          =     1.0235

------------------------------------------------------------------------------
             |             Robust HC2
           Y |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
           Z |   .5978652   .2047001     2.92   0.004     .1916445    1.004086
       _cons |   -.088036   .1475778    -0.60   0.552    -.3808994    .2048274
------------------------------------------------------------------------------

Diagnosis

. simulate p_value = r(p_value), reps(500): two_arm_design

      command:  two_arm_design
      p_value:  r(p_value)

Simulations (500)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5 
..................................................    50
..................................................   100
..................................................   150
..................................................   200
..................................................   250
..................................................   300
..................................................   350
..................................................   400
..................................................   450
..................................................   500

. 
. gen p_below_05 = p_value < .05

. 
. summarize p_below_05, meanonly

. 
. local power = round(r(mean), .001)

. 
. di "Power = `power'"
Power = .7000000000000001